Important Documents

Discrete Math Text - Digital
CoMap
CoMap
- Codebreaking
- The Math of Technology
Links
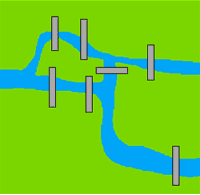
Königsberg Bridge Problem
In this puzzle we invite you to visit the bridges of the medieval city of Königsberg. Can you cross each bridge just once without missing any of them?
The Pregel River had two branches and flowed around an island through the center of the city of Königsberg. There were seven bridges connecting the various landmasses, as shown in this diagram.
The townspeople, who liked to stroll over the bridges, tried to figure out a path that would cross each of the seven bridges just once. You couldn’t miss any of the bridges, and you couldn’t cross any bridge more than once.
In this puzzle we invite you to visit the bridges of the medieval city of Königsberg. Can you cross each bridge just once without missing any of them?
The Pregel River had two branches and flowed around an island through the center of the city of Königsberg. There were seven bridges connecting the various landmasses, as shown in this diagram.
The townspeople, who liked to stroll over the bridges, tried to figure out a path that would cross each of the seven bridges just once. You couldn’t miss any of the bridges, and you couldn’t cross any bridge more than once.
Wolfram Projects - Demonstrations

Click on the picture to try the Tower of Hanoi

The Tower of Hanoi
The puzzle was invented by the French mathematician Édouard Lucas in 1883. There is a legend about an Indian temple which contains a large room with three time-worn posts in it surrounded by 64 golden disks. Brahmin priests, acting out the command of an ancient prophecy, have been moving these disks, in accordance with the rules of the puzzle, since that time. The puzzle is therefore also known as the Tower of Brahma puzzle. According to the legend, when the last move of the puzzle is completed, the world will end. It is not clear whether Lucas invented this legend or was inspired by it.
If the legend were true, and if the priests were able to move disks at a rate of one per second, using the smallest number of moves, it would take them (2^64)−1 seconds or roughly 585 billion years; it would take 18,446,744,073,709,551,615 turns to finish.
The puzzle was invented by the French mathematician Édouard Lucas in 1883. There is a legend about an Indian temple which contains a large room with three time-worn posts in it surrounded by 64 golden disks. Brahmin priests, acting out the command of an ancient prophecy, have been moving these disks, in accordance with the rules of the puzzle, since that time. The puzzle is therefore also known as the Tower of Brahma puzzle. According to the legend, when the last move of the puzzle is completed, the world will end. It is not clear whether Lucas invented this legend or was inspired by it.
If the legend were true, and if the priests were able to move disks at a rate of one per second, using the smallest number of moves, it would take them (2^64)−1 seconds or roughly 585 billion years; it would take 18,446,744,073,709,551,615 turns to finish.
Mega Penny Project

MegaPenny site
What does 1 Quadrillion pennies look like?
The Secret Universe Within - Multiples of 10
What does 1 Quadrillion pennies look like?
The Secret Universe Within - Multiples of 10
Circuits

Euler
Hamiltonian
Hamiltonian Circuit - Algorithms
click picture for link
click picture for link
Urban Planning Project - assignments
- Designing Your Own City: Maps and Google Sketchup
- The Unsuspecting Bridge Inspector: Eulerizing the Königsberg Bridge
- Designing Recycling Routes: Onitsha, Ghana
- What's the Shortest Route?: A Hamiltonian Circuit between all the cities in the class - include NNA, Brute Force Trees, and final optimized answer.
- Bus Route: Setup Optimized routes for bus lines that cover 75%+ of your cities streets.
- Tendency To Be Tardy: Using A2Tech layout (link), layout a critical path between any two classrooms and find a maximum passing time needed. (Need hallway measurements, walking times etc)
- Ted the Taxi Man: Euler circuit of the city for coverage and pickups, then Hamiltonian for a teacher set 5 point driving tour with ETA.
- Transportation Dilemma: Scheduling
Urban Planning Project - Resources

The Urban Planning Project - Wiki
Every thing you need to know about the project.
We will publish materials here when the project is complete.
Webquest - Construction
Building a Sustainable (Green) City Urban Spawl
Every thing you need to know about the project.
We will publish materials here when the project is complete.
Webquest - Construction
Building a Sustainable (Green) City Urban Spawl
Estate Division

Estate Division
Rent Division
Chore Division
The Moving Knife - physical division.
Rent Division
Chore Division
The Moving Knife - physical division.
| fairdivision_2011.ppt | |
| File Size: | 640 kb |
| File Type: | ppt |
Voting Theory


Voting Visualization: Borda, Condorcet, RO, SRO, Plurality, and Approval

Electoral College
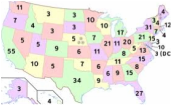
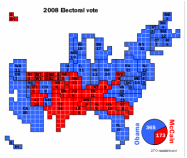
Electoral College votes by state - U.S. Map scaled by population. KEY: 1 grid square per vote (or IR multiple).
Code Breaking

Code Breaking WebQuest and information source
Codebreaking - how it works

Enigma Machine/History

Overview of WW2 codebreaking
DvD encryption and general codebreaking
Overview of Codebreaking - Ohio State
DvD encryption and general codebreaking
Overview of Codebreaking - Ohio State
Cryptography


Facial Recognition

Codebreaking Challenge

CodeBreaking

Try your skillz here.

Game Theory

Info
http://www.gametheory.net/
http://en.wikipedia.org/wiki/List_of_games_in_game_theory
Courses in Game Theory
http://oyc.yale.edu/economics/econ-159
https://www.coursera.org/course/gametheory
http://www.gametheory.net/
http://en.wikipedia.org/wiki/List_of_games_in_game_theory
Courses in Game Theory
http://oyc.yale.edu/economics/econ-159
https://www.coursera.org/course/gametheory
Class Presentations and Math Casts

Seige Math wiki
